���}Ŀ����D1���������߅��OABC���������OA=a�������OC=5�������BC=3,��AOC=��BCO=90�㣬���^�cO��ֱ��l����߅�ηֳɃɲ����������ֱ��l�cOC���ɵĽ��O��ȣ�����߅��OABC��ֱ�ǡ�OCB��ֱ��l�ۯB��������cC�����cD̎����D1����
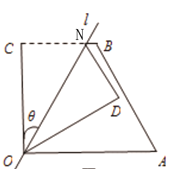
�D1 �D2 �D3
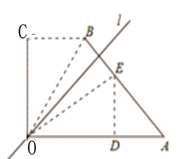
��1������=45�����������߅��OABC��ֱ�ǡ�OCB��ֱ��l�ۯB����������cB�����c��߅��OABC��߅AB�� (��D2) ���������a��ֵ. 
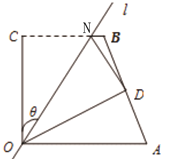
��2�����ۯB���cDǡ��AB�����c����D3�����������ȵ�ֵ�������
